Convolución de Pulso unitario trasladado
Dado un número real c positivo o negativo, denótese por δc al pulso unitario localizado en t=c; esto es
Dada una señal x(t), usando:
y la propiedad de traslación:
se tiene:
En consecuencia, formar la convolución de x(t) con el pulso unitario trasladado es equivalente a trasladar c segundos x(t).
Función Delta Dirac
La delta de Dirac o función delta de Dirac es una distribución o función generalizada introducida por primera vez por el físico inglés Paul Diracy, como distribución, define un funcional en forma de integral sobre un cierto espacio de funciones. Se escribe como:
Siendo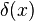 
la función tiende a infinito cuando x = 0, y para cualquier otro valor de x es 0.
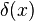la función tiende a infinito cuando x = 0, y para cualquier otro valor de x es 0.
Reemplazando la función Delta Dirac obtenemos=
Evaluamos x(0)=
Cultura General
PAUL DIRAC
Paul Dirac nació en Brístol (Inglaterra). Su padre, Charles, fue un inmigrante del cantón suizo de Valais que enseñaba francés. Su madre, originaria de Cornualles, era hija de marineros. Paul tenía una hermana pequeña y un hermano mayor Felix, que se suicidó. Él describió su infancia como infeliz, por la severidad y autoritarismo de su padre. Una reciente biografía ha matizado tal carácter, haciendo referencia al propio carácter difícil y taciturno de Paul.
Estudió en la Bishop Primary School y en el Merchant Venturers Technical College, una institución de la universidad de Brístol, que enfatizaba las ciencias modernas (algo inusual en la época, y a lo que Dirac estaría siempre agradecido).
Se graduó en ingeniería eléctrica en la universidad de Brístol en 1921. Tras trabajar poco tiempo como ingeniero, Dirac decidió que su verdadera vocación eran las matemáticas. Completó otra carrera en matemáticas en Brístol en 1923 y fue entonces admitido en la Universidad de Cambridge, donde desarrollaría la mayor parte de su carrera. Empezó a interesarse por la Teoría de la relatividad y el naciente campo de la física cuántica, y trabajó bajo la supervisión de Ralph Fowler.
BIBLIOGRAFIA
INTRODUCCION A SEÑALES Y SISTEMAS-EDWARD W. KAMEN
http://es.wikipedia.org/wiki/Delta_de_Dirac
http://es.wikiquote.org/wiki/Paul_Dirac
No hay comentarios:
Publicar un comentario